On the premise that the charged particle is a normal geometry model, an expression of the migration current, displacement current and magnetic induction intensity generated by the charged particle motion is deduced according to the microscopic definition of current intensity, the total current law and the Biot-Savart law. Further calculate the electric field force between two charged particles in vacuum, give the velocity constraint relationship and velocity value criterion of the electric and magnetic field forces, and compare the consistency with the correlation results obtained considering the relativistic effect. It is pointed out that the magnetic field force is comparable to the electric field force only when the charged particle moves near the speed of light.
| Published in | American Journal of Physics and Applications (Volume 12, Issue 2) |
| DOI | 10.11648/j.ajpa.20241202.11 |
| Page(s) | 21-26 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2024. Published by Science Publishing Group |
Motor Charge, Migration Current, Displacement Current, Speed of Light
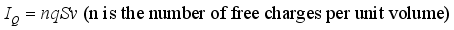 (1)
(1) 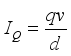 (2)
(2) 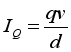 (3)
(3) 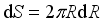 , the Angle between the direction of the normal and the direction of the electric field is ф and the electric field intensity at the surface element is
, the Angle between the direction of the normal and the direction of the electric field is ф and the electric field intensity at the surface element is 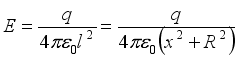 (4)
(4) 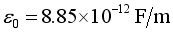 , it is called the vacuum dielectric constant (the same below).
, it is called the vacuum dielectric constant (the same below). 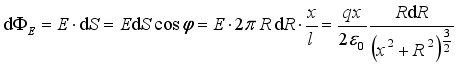 (5)
(5) 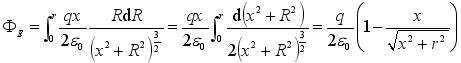 (6)
(6) 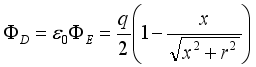 (7)
(7) 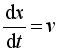 , it is not difficult to conclude that the displacement current passing through the loop is
, it is not difficult to conclude that the displacement current passing through the loop is 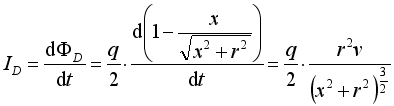 (8)
(8) 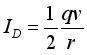 (9)
(9) 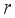
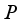 Find out. As shown in Figure 2, the magnetic induction intensity at a point from the moving charged particle (the velocity vertical to the particle) is
Find out. As shown in Figure 2, the magnetic induction intensity at a point from the moving charged particle (the velocity vertical to the particle) is 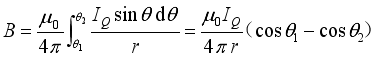 (10)
(10) 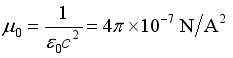 Where, it is the vacuum permeability (the same below). Considering that in practical situations,
Where, it is the vacuum permeability (the same below). Considering that in practical situations, 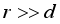 ,
, 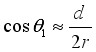 ,
, 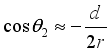 Therefore, formula (10) can be rewritten as
Therefore, formula (10) can be rewritten as 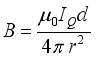 (11)
(11) 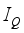 is determined by the formula (2). Therefore, by substituting formula (2) into formula (11), the
is determined by the formula (2). Therefore, by substituting formula (2) into formula (11), the 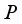 pmagnetic induction strength at the available point is
pmagnetic induction strength at the available point is 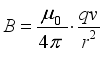 (12)
(12) 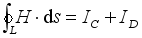 (13)
(13) 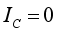 , the formula (13) can be reduced to
, the formula (13) can be reduced to 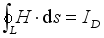 (14)
(14) 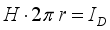 (15)
(15) 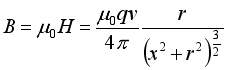 (16)
(16) 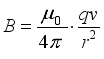 (17)
(17) 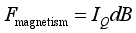 (18)
(18) 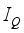 is determined by formula (2) and the magnetic induction strength B is determined by formula (12). Therefore, combining (2) and (12), (18) can be rewritten as
is determined by formula (2) and the magnetic induction strength B is determined by formula (12). Therefore, combining (2) and (12), (18) can be rewritten as 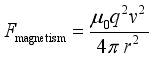 (19)
(19) 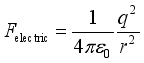 (20)
(20) 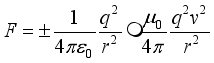 (21)
(21) 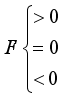 (22)
(22) 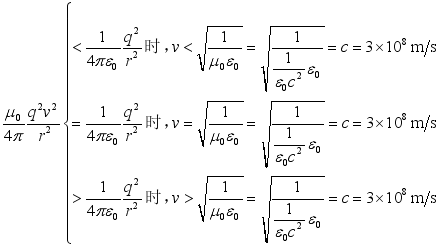 (23)
(23) 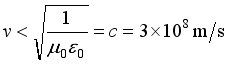
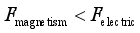 At that time, the effect between the two particles was repulsion (attraction).
At that time, the effect between the two particles was repulsion (attraction). 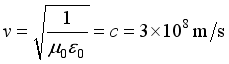
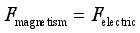 At that time, the effect between the two particles behaved as zero. According to the current support theory, this situation is difficult or even impossible to achieve.
At that time, the effect between the two particles behaved as zero. According to the current support theory, this situation is difficult or even impossible to achieve. 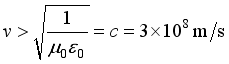
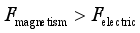 At that time, the action between the two particles appeared as attraction (repulsion). Of course, according to the current support theory, this situation does not exist.
At that time, the action between the two particles appeared as attraction (repulsion). Of course, according to the current support theory, this situation does not exist. 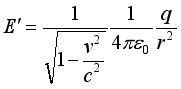 (24)
(24) 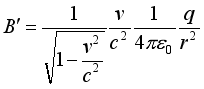 (25)
(25) 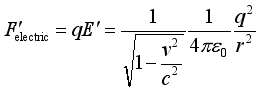 (26)
(26) 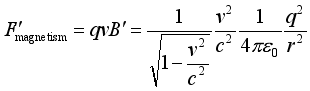 (27)
(27) 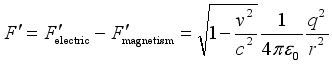 (28)
(28) 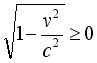 (29)
(29) 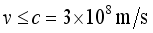 (30)
(30) 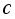
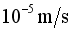 order of magnitude) is very small, and the distance between the wires (usually about 1-3m) is relatively large. Therefore, the current and magnetic field forces between them are very weak, and their unit length is generally only
order of magnitude) is very small, and the distance between the wires (usually about 1-3m) is relatively large. Therefore, the current and magnetic field forces between them are very weak, and their unit length is generally only 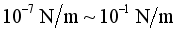 , and they will not have adverse accidents because of the current and magnetic field between each other.
, and they will not have adverse accidents because of the current and magnetic field between each other. | [1] | Zhao Kaihua, Chen mou. New Concept physics tutorial on Electromagnetism (second edition) [M]. Beijing: Higher Education Press, 2006. 12(2): 109-113. |
| [2] | Miao Zhongying. Discussion of electromagnetics issues [M]. Anhui: University of Science and Technology of China University Press, 2018 (1): 239-240. |
| [3] | Zhang Sanhui. University of Physics (Mechanics, electromagnetism) [M]. Beijing: Tsinghua University Press, 2009. 2(3): 343-344. |
| [4] |
Available from:
https://baike.baidu.com/item/%E5%85%A8%E7%94%B5%E6%B5%81%E5%AE%9A%E5%BE%8B/7202859?fr=ge_ala- [On May 23, 2024] |
| [5] | Available from: |
| [6] |
Available from:
https://www.eefocus.com/baike/1518246.html [On September 9, 2024] |
| [7] |
Available from:
https://zhidao.baidu.com/question/1808749723296596747.html [On September 9, 2024] |
| [8] |
Available from:
https://zhidao.baidu.com/question/1650406998265661260.html [On September 9, 2024] |
| [9] |
Available from:
https://www.docin.com/p-2066621658.html [On September 9, 2024] |
| [10] | Available from: |
| [11] | Guo Shuohong. Electrodynamics (Third Edition) [M]. Beijing: Higher Education Press, 2008. 6(3): 217-222. |
| [12] | Cao Changqi. Electrodynamics [M]. Beijing: People's Education Press, 1962. 7(2): 281-289. |
| [13] | Li Yuanjie. electrodynamics [M]. Beijing: Machinery Press, 2014. 7(1): 136-144. |
| [14] | Wang Zhi shi. A concise tutorial of electrodynamics [M]. Chengdu: Sichuan University Press, 1996. 8(1): 152-163. |
| [15] | Ding Mingxin. Electrodynamics [M]. Shenyang: Liaoning Education Press, 1986. 11(1): 512-530. |
| [16] | Ren Yi Zhi. A concise tutorial of electrodynamics [M]. Tianjin: Nankai University Press, 2003. November (1): 223-245. |
| [17] | Cheng Jinglong, Wu Xiaosong. On charge attraction or repulsion and related issues [J]. Physical Bulletin, 2017. 2: 110-112. |
APA Style
shu, H. S., jie, F. J. (2024). Quantitative Investigation of Parallel Interactions Between Charged Particles. American Journal of Physics and Applications, 12(2), 21-26. https://doi.org/10.11648/j.ajpa.20241202.11
ACS Style
shu, H. S.; jie, F. J. Quantitative Investigation of Parallel Interactions Between Charged Particles. Am. J. Phys. Appl. 2024, 12(2), 21-26. doi: 10.11648/j.ajpa.20241202.11
@article{10.11648/j.ajpa.20241202.11,
author = {Huang Shao shu and Feng Jun jie},
title = {Quantitative Investigation of Parallel Interactions Between Charged Particles
},
journal = {American Journal of Physics and Applications},
volume = {12},
number = {2},
pages = {21-26},
doi = {10.11648/j.ajpa.20241202.11},
url = {https://doi.org/10.11648/j.ajpa.20241202.11},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ajpa.20241202.11},
abstract = {On the premise that the charged particle is a normal geometry model, an expression of the migration current, displacement current and magnetic induction intensity generated by the charged particle motion is deduced according to the microscopic definition of current intensity, the total current law and the Biot-Savart law. Further calculate the electric field force between two charged particles in vacuum, give the velocity constraint relationship and velocity value criterion of the electric and magnetic field forces, and compare the consistency with the correlation results obtained considering the relativistic effect. It is pointed out that the magnetic field force is comparable to the electric field force only when the charged particle moves near the speed of light.
},
year = {2024}
}
TY - JOUR T1 - Quantitative Investigation of Parallel Interactions Between Charged Particles AU - Huang Shao shu AU - Feng Jun jie Y1 - 2024/09/23 PY - 2024 N1 - https://doi.org/10.11648/j.ajpa.20241202.11 DO - 10.11648/j.ajpa.20241202.11 T2 - American Journal of Physics and Applications JF - American Journal of Physics and Applications JO - American Journal of Physics and Applications SP - 21 EP - 26 PB - Science Publishing Group SN - 2330-4308 UR - https://doi.org/10.11648/j.ajpa.20241202.11 AB - On the premise that the charged particle is a normal geometry model, an expression of the migration current, displacement current and magnetic induction intensity generated by the charged particle motion is deduced according to the microscopic definition of current intensity, the total current law and the Biot-Savart law. Further calculate the electric field force between two charged particles in vacuum, give the velocity constraint relationship and velocity value criterion of the electric and magnetic field forces, and compare the consistency with the correlation results obtained considering the relativistic effect. It is pointed out that the magnetic field force is comparable to the electric field force only when the charged particle moves near the speed of light. VL - 12 IS - 2 ER -